In this article, we’re gonna being continuing off the first part where we got from O(2^n) to O(n) time complexity using memoization.

Where we left off:

The algorithm we had developed looked like this:

memo = {1: 1, 2: 1}
def fib(n):
  if (n in memo): return n
  
  memo[n] = fib(n - 1) + fib(n - 2)
  return memo[n]

it took about 337 microseconds to calculate fib(1000) . We’ll be continuing from here.

Leaving recursion: A faster non-recursive solution

While our recursive solution is definitely more elegant and intuitive to understand, we have a big problem. While it has a time complexity of O(n), it also has a space complexity of O(n). Space complexity refers to how big the memory usage of our algorithm increases with as our input size increases. While a space complexity of O(n) is still fine, we can do better. Also, with n = 1000, our memo dictionary will become so big that the algorithm will waste time just searching whether or not our n is in the memo in our if statement. We can do better.

We begin by having just 2 variables: prev , and curr . The curr variable stores the current number in the sequence, the prev variable stores the previous number.

At the start, we begin with prev and currboth being 1.

Finally, we’ll need an index variable to know which number in sequence we’re currently at. We’ll begin with the third number since the first two numbers are already taken care of from our if statement.

def fib(n):

  prev = 1
  curr = 2

  idx = 3

Then we loop till our idx variable reaches n. In the loop we have 3 calculations:

• Increment the curr variable with the prev variable
• Set the prev variable to what the curr variable. In this case, we need a temp variable to store what the curr variable was, since we’re changing the curr variable.
• Increment our idx variable by 1

while (idx <= n):
    temp = curr_num
    curr_num += prev_num
    prev_num = temp
    idx+=1

Finally, we just return the current variable after the loop is done

return curr_num

Final code:

def fib(n):
    prev_num = 1
    curr_num = 1
    idx = 3
    while (idx <= n):
        temp = curr_num
        curr_num += prev_num
        prev_num = temp
        idx+=1
    return curr_num

This takes our time taken from about 337 microseconds to about 100 microseconds. But we need to go faster!

Coming back to recursion: The fast doubling algorithm

I’m going begin this algorithm by introducing you to two identities that some smart folks have found out in the fibonacci sequence.

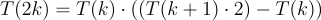
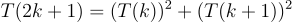
These equations tell us that if we have the kth and the (k+1)th term, we can find the 2kth and the (2k+1)th term. Now, we can use the same identities to find the kth and the (k+1)th term given the (k//2)th and the (k//2 + 1)th term.

Note that this is integer division. That means, it takes the floor of the actual division. So 7//2 = 3, 13 // 3 = 4

So, how can we use this to calculate fib(n) . Okay, suppose we have a number k . To calculate fib(k) , we first find fib(k//2) and fib(k//2 + 1) . Then using those two identities, we can calculate fib(k) and fib(k+1) . But to calculate fib(k//2) and its successor, we again perform fib(k//2//2) . We do this until we get to the base case, which, in this case is 0. Now notice also that at each time, we need two values, fib(k//2) and fib(k//2+1) to calculate fib(k) . So, at all times, our function will output those two numbers.

Our code till now is:

def fib(n):
    if (n == 0): return (0, 1) # Base case: (fib(0), fib(1))

    a, b = fib(n // 2) # Assuming that our function returns 2 numbers

Also notice that if k is odd, k//2 is actually k/2-0.5 . Using those two identities, we get the element at the 2*(k/2-0.5) = k-1 element. So, if k is odd, our function returns fib(k-1) and fib(k) rather than fib(k) and fib(k+1) like it should. But no worries, we know the recursive definition of the fibonacci sequence: fib(k+1) = fib(k) + fib(k-1) , so we can get fib(k+1) from there.

c = a * ((b * 2) - a)
d = (a * a) + (b * b)

Then using those two identities, we calculate fib(k) and fib(k+1) . Though if k is odd, then we actually get fib(k-1) and fib(k) . Let’s denote the results of those calculations as c and d . If k is even, then we can simply return (c, d) . But, if k is odd, we need to return d and its successor, which is (from the fib recursive definition), c+d . So we return c, c+d)

if (n % 2 == 0):
    return (c, d)
else:
    return (d, c + d)

Full Code:

def fib(n):
    if (n == 0): return (0, 1) # (F(0), F(1))

    a, b = fib(n // 2)

    c = a * ((b << 1) - a)
    d = (a * a) + (b * b)

    if (n % 2 == 0):
        return (c, d)
    else:
        return (d, c + d)

Finally, note how I replaced b*2 with b<<1 . The << is called the left bitshift operator. All it does is take the binary and shift each bit to the left by 1. Since binary is a base 2 number system, shifting each bit to the left by 1 has the same effect as multiplying by 2, though is faster.

How fast is this algorithm?

Well, pretty fast.

CPU times: user 2 µs, sys: 1 µs, total: 3 µs
Wall time: 5.01 µs

Sometimes, I also get such crazy times from the algorithm:

CPU times: user 1e+03 ns, sys: 0 ns, total: 1e+03 ns
Wall time: 2.86 µs

So, safe to say the extra work and the clever insights were worth it.

Why O(log n) complexity?

For O(2^n) complexity, remember that at each step, we were multiplying the problem and making it bigger and bigger till we reach the base case. In this case, we’re doing the opposite. Since we’re dividing by 2 each time, we’re dividng the problem by 2 every function call. And algorithms which do that tend to have O(log n) time complexity. Note: This is log base 2 and not log base 10.

Conclusion

With the fast doubling algorithm, we’ve significantly improved the efficiency of computing Fibonacci numbers. From the naive O(2^n) algorithm, through memoization to O(n), and finally to the fast doubling method with O(log n), we’ve seen how mathematical insights and clever algorithm design can lead to substantial performance gains. This progression highlights the importance of exploring different approaches and leveraging mathematical properties for optimizing algorithms.